Exercícios: Geometria Plana

Exercícios de Geometria Plana

1) Determine a área das seguintes figuras (em cm): a) b)    c)  d)  e)                  2) Temos um triângulo equilátero de lado 6cm. Qual é o perímetro e qual é a área deste triângulo? 3) Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a altura igual a 10. Qual a área deste trapézio? 4) Sabendo que a área de um quadrado é 36cm², qual é seu perímetro? 5) Calcule a área e o perímetro (em metros) dos retângulos descritos: a) a = 25 e b = 12 b) a = 14 e b = 10

Vídeo Quadriláteros - Losango

https://www.youtube.com/watch?v=BWWaSz-X6nM

Losangulo

Losango

Quadrilátero equilátero, ou seja, formado por quatro lados iguais, o losango, junto com o quadrado e o retângulo, é considerado um paralelogramo.

Ou seja, é um polígono de quatro lados os quais possuem lados e ângulos opostos congruentes e paralelos.O Losango é uma figura geométrica plana representada por um quadrilátero equilátero, ou seja, um polígono formado por quatro lados iguais.

Importante destacar que todo losango é um paralelogramo, cujos lados opostos são iguais e paralelos, com duas diagonais que se cruzam perpendicularmente.

Diferente do quadrado, que possui quatro ângulos iguais a 90º, o losango possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).

Assim, enquanto o losango é um paralelogramo composto de quatro lados congruentes, o retângulo é um paralelogramo composto de quatro ângulos congruentes. Já o quadrado é um paralelogramo composto de quatro lados e quatro ângulos congruentes.

Saiba mais sobre o Paralelogramo e a Área do Paralelogramo.

Fórmula da Área

Para calcular a área do losango é necessário traçar duas diagonais. Dessa forma tem-se 4 triângulos retângulos (com ângulo reto de 90º) iguais.

Assim, podemos encontrar a área do losango a partir da área de 4 triângulos retângulos ou 2 retângulos.Assim, a fórmula para encontrar a área do losango é representada da seguinte maneira:

Sendo A, a área do losango, D1 a diagonal maior e D2 a diagonal maior.

Vídeo aula sobre trapézio

https://www.youtube.com/watch?v=2IPnbQmO88Y

Trapézio

Trapézio

Chamado de quadrilátero notável, pois a soma dos seus ângulos internos corresponde a 360º, o trapézio é uma figura geométrica plana.

Ele possui dois lados e bases paralelas, donde uma é maior e outra menor. São classificados em:

• trapézio retângulo: possui dois ângulos de 90º;
• trapézio isósceles ou simétrico: os lados não paralelos possuem a mesma medida;
• trapézio escaleno: todos os lados de medidas diferentes.A área do trapézio mede o valor da superfície dessa figura plana formada por quatro lados.
  O trapézio é um quadrilátero que possui dois lados e duas bases paralelas, sendo que uma é maior e outra menor.
  O trapézio é considerado um quadrilátero notável, de forma que a soma de seus ângulos internos corresponde a 360°.

  Classificação dos Trapézios

  Os trapézios são classificados em três tipos:
  
  • Trapézio Retângulo: apresenta dois ângulos de 90º, chamados de ângulos retos.
  • Trapézio Isósceles ou Simétrico: os lados não paralelos são congruentes (possuem a mesma medida).
  • Trapézio Escaleno: todos os lados possuem medidas diferentes.

  Fórmula da Área

  Para calcular a área do trapézio utilizamos a seguinte fórmula:
  
  Onde:
  A: área da figura
  B: base maior
  b: base menor
  h: altura
  

  Fórmula do Perímetro

  Para calcular o perímetro do trapézio utiliza-se a fórmula:
  P = B + b + L1 + L2
  Donde:
  P: perímetro (soma de todos os lados)
  B: base maior
  b: base menor
  L1 e L2: lados da figura

Vídeo, área e perímetro de um círculo

https://www.youtube.com/watch?v=bqJ2nn16j60

Círculo

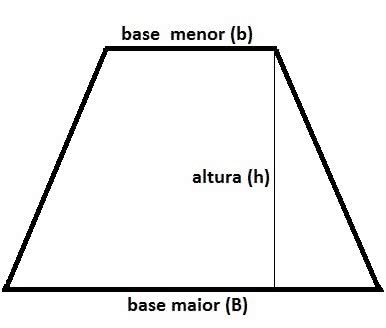
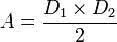Círculo

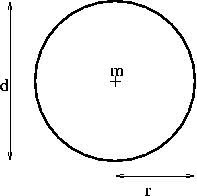
Figura geométrica plana caracterizada pelo conjunto de todos os pontos de um plano. O raio (r) do círculo corresponde a medida da distância entre o centro da figura até sua extremidade.

A área do círculo corresponde ao valor da superfície dessa figura, levando em conta a medida de seu raio (r).

O que é Círculo?

Vale lembrar que o círculo, também chamado de disco, é uma figura geométrica que faz parte dos estudos da geometria plana.

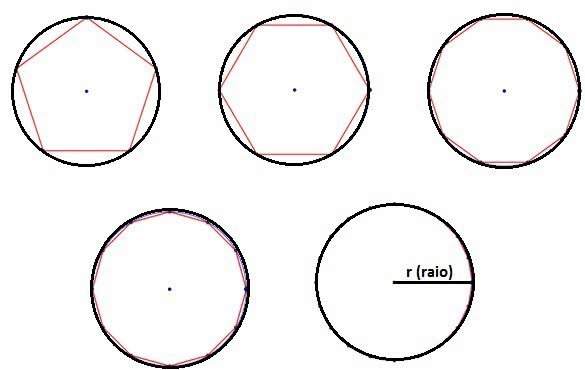
Essa figura surge na medida em que os polígonos regulares inscritos nela vão aumentando o número dos lados.

Ou seja, com o aumento do número de lados dos polígonos estes vão se aproximando da forma circular.

Fórmula: Cálculo da Área do Círculo

Para calcular a área do círculo devemos utilizar a seguinte fórmula:

A = π . r2

Donde,

π: constante Pi (3,14)
r: raio

Fique Atento!

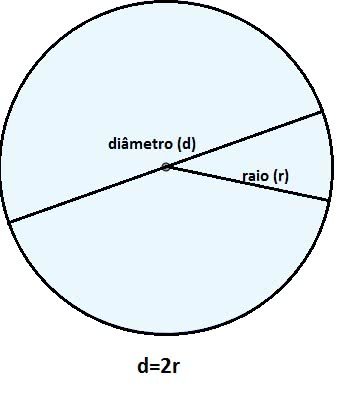
Lembre-se que o raio (r) corresponde a distância entre o centro e a extremidade do círculo.

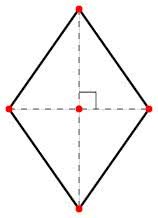
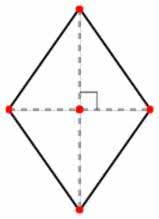
Já o diâmetro é um segmento de reta que passa pelo centro do círculo, dividindo-o em duas metades iguais. Dito isso, o diâmetro equivale duas vezes o raio (2r).

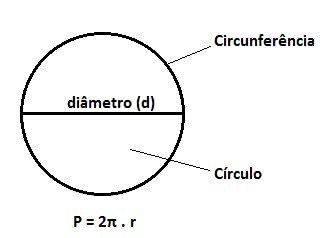
Perímetro do Círculo

O perímetro é um conceito da matemática que mede o comprimento (contorno) de determinada figura. Em outras palavras, o perímetro é a soma de todos os lados de uma figura geométrica.

No caso do círculo, o perímetro é chamado de circunferência e é calculado pelo dobro da medida do raio (2r). Assim, o perímetro da circunferência é medido pela fórmula:

P = 2 π . r

Vídeo sobre área e perimetro do Quadrado

Quadrado

Quadrado

Quadrado

Polígono de quatro lados iguais, o quadrado ou quadrilátero é uma figura geométrica plana que possuem os quatro ângulos congruentes: retos (90°).

Perímetro do Quadrado

O perímetro do quadrado corresponde a soma dos quatro lados dessa figura plana.

Lembre-se que o quadrado é um quadrilátero regular que apresenta lados com as mesmas medidas (congruentes). Assim, essa figura é composta por quatro ângulos retos (90°).

Fórmula do Perímetro

O perímetro do quadrado é calculado utilizando a fórmula:

P = L + L + L + L
ou
P = 4L

Fórmula da Área

Diferente do perímetro, a área é a medida da superfície da figura. Assim, a área do quadrado é calculada pela fórmula:

A = L2

Video sobre triangulos

Triâgulos

Triângulo

Polígono (figura plana fechada) de três lados, o triângulo é uma figura geométrica plana formada por três segmentos de reta.

Segundo a forma dos triângulos, eles são classificados em:

• triângulo equilátero: possui todos os lados e ângulos internos iguais (60°);
• triângulo isósceles: possui dois lados e dois ângulos internos congruentes;
• triângulo escaleno: possui todos os lados e ângulos internos diferentes.

No tocante aos ângulos que formam os triângulos, eles são classificados em:

• triângulo retângulo: possui um ângulo interno de 90°;
• triângulo obtusângulo: possui dois ângulos agudos internos, ou seja, menor que 90°, e um ângulo obtuso interno, maior que 90°;
• triângulo acutângulo: possui três ângulos internos menores que 90°.

Figuras da Geometria Plana

Introdução à ângulos geometria plana

Geometria Plana

Geometria Plana

A geometria plana ou euclidiana é a parte da matemática que estuda as figuras que não possuem volume.

A geometria plana também é chamada de euclidiana, uma vez que seu nome representa uma homenagem ao geômetra Euclides de Alexandria, considerado o “pai da geometria”.

Curioso notar que o termo geometria é a união das palavras “geo” (terra) e “metria” (medida); assim, a palavra geometria significa a "medida de terra".

Conceitos de Geometria Plana

Alguns conceitos são de suma importância para o entendimento da geometria plana, a saber:

Ponto

Conceito adimensional, uma vez que não possui dimensão. Os pontos determinam uma localização e são indicados com letras maiúsculas.

Reta

A reta, representada por letra minúscula, é uma linha ilimitada unidimensional (possui o comprimento como dimensão) e pode se apresentar em três posições:

• horizontal
• vertical
• inclinada

Dependendo da posição das retas, quando elas se cruzam, ou seja, possuem um ponto em comum, são chamadas de retas concorrentes.

Por outro lado, as que não possuem ponto em comum, são classificadas como retas paralelas.

Segmento de Reta

Diferente da reta, o segmento de reta é limitado pois corresponde a parte entre dois pontos distintos.

A semirreta é limitada somente num sentido, visto que possui início e não possui fim.

Plano

Corresponde a uma superfície plana bidimensional, ou seja, possui duas dimensões: comprimento e largura. Nessa superfície que se formam as figuras geométricas.

Ângulos

Os ângulos são formados pela união de dois segmentos de reta, a partir de um ponto comum, chamado de vértice do ângulo. São classificados em:

• ângulo reto (Â = 90º)
• ângulo agudo (0º < Â < 90º)
• ângulo obtuso (90º < Â < 180º)

Área

A área de uma figura geométrica expressa o tamanho de uma superfície. Assim, quanto maior a superfície da figura, maior será sua área.

Perímetro

O perímetro corresponde a soma de todos os lados de uma figura geométrica.